jbvilla.blogg.se - Supplementary angle pairs

It should be noted that all linear pairs are supplementary because supplementary angles sum up to 180°.

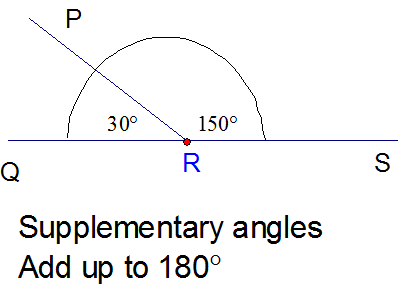
When two lines intersect each other, the adjacent angles make a linear pair. When the two angles share a common side, a common vertex, and they do not overlap, then the pairs of angles are always adjacent angles. What Pairs of Angles are Always Adjacent? When two angles are supplementary angles each angle is called the supplement of the other angle. It is not necessary that the angles must always be adjacent to each other, but their sum should always be 180°. Two angles are considered supplementary when they sum up to 180°. How Many Pairs of Angles are Supplementary? There are nine pairs of angles listed below: These topics will also give you a glimpse of how such concepts are covered in Cuemath.įAQs on Pairs of Angles How Many Pairs of Angles Are There? Given below is the list of topics that are closely connected to Pairs of Angles. However, the sum of the angles in both cases should always be 180°. Fact: All linear pairs are supplementary, but all supplementary angles need not be linear pairs.Mistake: All supplementary angles are linear pairs.Fact: For angles to be adjacent, they have to share a common side and vertex.Mistake: Any angles next to each other are adjacent angles.These angles need not be necessarily next to each other but their sum should be 90°. Fact: When the sum of two angles is 90°, the angles are called complementary angles.Mistake: Complementary angles have to be next to each other.Read the following points to overcome some common mistakes and know the real facts behind them. In the following figure, ∠1 and ∠2 are pairs of corresponding angles that are equal. Lie on the same side of the transversal, and lie above (or below) the lines.

Corresponding angles are the angles that: When a transversal intersects two parallel lines, the corresponding angles formed are always equal. In the following figure, ∠1 & ∠7, ∠2 & ∠8 are alternate exterior angles. Alternate-exterior angles are those angles that: When a transversal intersects two parallel lines, the alternate exterior angles formed are always equal. In the following figure, ∠4 and ∠6, ∠3 and ∠5 are the alternate interior angles.

Lie between the interior of the two lines.

Lie on the alternate sides of the transversal.

Alternate-interior angles are those angles that: When a transversal intersects two parallel lines, the alternate interior angles formed are always equal. Similarly, ∠4 and ∠5 are co-interior angles. In the following figure, ∠3 and ∠6 are co-interior angles.

Are on the same side of the transversal.

Co-interior angles are those angles that: When a transversal intersects two parallel lines, the co-interior angles are always supplementary. Let us discuss the pairs of angles formed by a transversal in detail. These pair of angles have a special relationship between them. In conclusion, doing this for each one of the pairs of sides gives the required proof.When 2 parallel lines are cut by a transversal, many pairs of angles are formed. And, we'll use one of the other sides as the transversal line. In other words, the two opposing sides will be used as the parallel lines. So, let's apply the above theorem to each pair of sides. We have already proven that for the general case of parallel lines, a transversal line creates interior angles that sum up to 180°.īut, a parallelogram is simply two pairs of parallel lines. Therefore, it's a simple use of the properties of parallel lines to show that the consecutive angles are supplementary. The definition of a parallelogram is that both pairs of opposing sides are parallel. Show that the pairs of consecutive angles are supplementary. We'll prove this property using one of the theorems about parallel lines - the Consecutive Interior Angles Theorem. This property will be very useful in many problems involving parallelograms. One of the basic properties of parallelograms is that any pair of consecutive angles are supplementary.